Red Neuronal Convolucional: Detección Fichas Mahjong

Tengo el objetivo de crear un algoritmo de reconocimiento de imágenes, fichas de Mahjong en este caso, mediante una Red Neuronal Convolucional (CNN). Utilizaremos Keras en Python. Este algoritmo nos servirá para introducir esta funcionalidad en la aplicación Mahjong Scoring MCR (https://play.google.com/store/apps/details?id=com.mahjongscoring.activities), y así poder contabilizar las distintas combinaciones de la mano ganadora y obtener la puntuación total de manera automática.

En este post vamos a ver un primer modelo de CNN con un puñado de imágenes, observaremos el grado de acierto de nuestro algoritmo y analizaremos visualmente cuales son sus fallos.

Antes de comenzar explicaremos que el Mahjong es un juego de 4 jugadores en el cual por turnos cada jugador, de manera individual, tiene que formar tríos y escaleras. Se puede decir que es una especie de juego de cartas tipo Chin Chon o Continental. Si queréis más información sobre el juego podéis pasaros por mi página web: https://www.mahjongmadrid.com/

El Mahjong consta de 4 palos o familias, con un total de 34 fichas distintas (sin contar las flores ni las estaciones). Para comenzar vamos a seleccionar solamente imágenes del palo de las ruedas, en total 9 fichas distintas. Tenemos 109 imágenes distintas de este palo de las cuales hay 4 copias, por lo que contamos con 436 imágenes en total. Son pocas imágenes, pero para nuestro modelo inicial servirá. Para la versión definitiva de nuestro modelo tenemos que obtener muchas más imágenes y haremos uso de Data Augmentation.

Podemos ver como hay imágenes de fichas físicas y otras imágenes de fichas digitales. Algunas tienen la insignia con el número. Esto puede complicar el acierto de nuestro algoritmo, lo veremos en detalle.

RED NEURONAL CONVOLUCIONAL

Estos son los pasos que vamos a seguir:

• Importar librerías
• Cargar y procesar las imágenes.
• Crear dinámicamente las etiquetas de resultado.
• Dividir en sets de Entrenamiento, Validación y Test
• Crear el modelo de la CNN
• Ejecutar nuestra máquina de aprendizaje (Entrenar la red)
• Revisar los resultados obtenidos

Empecemos a programar:

# Comenzamos importando las librerías que vamos a utilizar para el tratamiento de las imágenes.
import numpy as np
import glob
from skimage.io import imread
import os
from skimage.transform import resize
from sklearn.model_selection import train_test_split

# Definimos la función con las que vamos a procesar las imágenes
imagenes = []
y = []
def cargar(carpeta):
    lista = os.listdir(carpeta)
    for i in lista:
        image = imread(carpeta + i) # Lectura de cada imagen
        img_reducida = resize(image, (64, 64, 3), mode="reflect") # Definimos el tamaño
        img_normalizada = img_reducida.astype('float32') # Normalizamos 
        imagenes.append(img_normalizada) # Añadimos cada imagen procesada a la lista.
        y.append(i[0:1]) # Añadimos la primera letra del nombre de cada imagen que en este caso coindice con el número de la ficha que es.
    return imagenes, y

# Definimos la ruta de las imágenes
carpeta='...\\dirname'

# Leemos, guardamos y reducimos las imágenes, y lo convertimos en array
fichas = cargar(carpeta)
X = np.asarray(fichas)

# Mezclamos las imágenes para que estén ordenadas.
np.random.seed(8)
np.random.shuffle(X)
np.random.shuffle(y)

# Aunque tengamos pocas imágenes vamos a dividir el set de datos en 75-25 para entrenamiento y para test. A su vez, el conjunto de entrenamiento también lo subdividiremos en otro 80-20 para Entrenamiento y Validación en cada iteración (EPOCH) de aprendizaje.

# Separamos nuestras imágenes en el conjunto de train y de test:
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.25, random_state=8)

# Guardamos las imáneges procesadas para poder utilizarlas en el momento preciso
datafile = '...\\dirname\\ruedas.npz'  
np.savez(datafile, X_train=X_train, y_train=y_train, X_test=X_test, y_test=y_test)

# Cargamos las imágenes en caso de ser necesario
datafile2 = '...\\dirname\\ruedas.npz'
data = np.load(datafile2)

X_train = data['X_train']
X_test = data['X_test']
y_train = data['y_train']
y_test = data['y_test']

# Revisamos que este todo correcto
print(X_train.shape)
print(y_train.shape)

print(X_test.shape)
print(y_test.shape)

(327, 64, 64, 3)
(327,)
(109, 64, 64, 3)
(109,)

Crearemos las etiquetas en labels , es decir, le daremos valores de 1 al 9 a cada ficha. Esto lo hacemos para poder usar el algoritmo supervisado e indicar que cuando cargamos una imagen del 1 de ruedas en la red, ya sabemos que corresponde con la “etiqueta 1”. Y con esa información, entrada y salida esperada, la red al entrenar, ajustará los pesos de las neuronas.

Ademas haremos el “One-Hot encoding” con to_categorical() que se refiere a convertir las etiquetas (nuestras clases) por ejemplo el 6 de ruedas que es un 6 a una salida de tipo (0 0 0 0 0 0 1 0 0 0). Esto es porque así funcionan mejor las redes neuronales para clasificar y se corresponde con una capa de salida de la red neuronal de 10 neuronas.

# Importamos la librería necesaria
from keras.utils import to_categorical

# Cambiamos labels utilizando one-hot encoding
train_Y_one_hot = to_categorical(y_train)
test_Y_one_hot = to_categorical(y_test)

# Comprobamos con un ejemplo
print(y_train[7])
print(train_Y_one_hot[7])

6
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]

RED NEURONAL CONVOLUCIONAL

# Cargamos librerias

from keras.models import Sequential,Input,Model
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.layers.advanced_activations import LeakyReLU
from keras.models import save_model, load_model

Para llegar al modelo que presento a continuación hemos seguido los siguientes pasos:

Nuestra primera red es una toma de contacto y me sirve para ver que todo está en su sitio. Es una red muy básica con estas capas:

• Convolution2D (32 filtros, kernel 3x3, valid, e imágenes (64x64x3)
• Activación RELU
• MaxPooling2D
• Flatten
• Dropout (0.25)
• Dense (2, sigmoid)

Además, tiene un batch_size de 128 y 20 épocas (Estos parámetros se mantendrán inalterables en la fase 1 y 2). En el compile siempre incluimos categorical_crossentropy, optimizador Adam y como métrica accuracy.

Con esta primera red conseguimos cerca de un 0.4% de accuracy. Viendo el mal resultado de esta red comenzamos a introducir más capas que ayuden a nuestro modelo, incluimos otra capa de Convolution2D con activación RELU y otra MaxPooling, quedando algo parecido a esto:

• Convolution2D (32 filtros, kernel 3x3, valid, (64x64x3))
• Activación RELU
• MaxPooling2D
• Convolution2D (64 filtros, kernel 3x3, valid, (64x64x3))
• Activación RELU
• MaxPooling2D
• Flatten
• Dropout (0.25)
• Dense (10, softmax)

Con esto termina la primera fase con la que no consigo buenos resultados, teniendo entre un 0.5 y 0.6 de accuracy.

Viendo la mejora de nuestro modelo según vamos incluyendo nuevas capas, optamos por incluir todas las capas Convolution2D posibles y tras esta una capa MaxPooling. Esto hace mejorar nuestro modelo considerablemente. Vemos que al incluir un Dropout intermedio el modelo también mejora. En un primer momento lo incluimos de 0.5 pero llegamos a la conclusión que es demasiado alto y está dificultando enormemente el entrenamiento de nuestro modelo. El que si aumentamos hasta el 0.5 es el que se encuentra en la parte final ya que esto nos ayuda a evitar el sobreajuste.

En este punto tenemos una red parecida a esto:

• Convolution2D (32 filtros, kernel 3x3, valid, (64x64x3), ReLU)
• MaxPooling2D
• Convolution2D (64 filtros, kernel 3x3, valid, (64x64x3), ReLU)
• MaxPooling2D
• Convolution2D (128 filtros, kernel 3x3, valid, (64x64x3), ReLU)
• Dropout (0.2)
• MaxPooling2D
• Convolution2D (256 filtros, kernel 3x3, valid, (64x64x3), ReLU)
• MaxPooling2D
• Flatten()
• Dropout (0.5)
• Dense (10, softmax)

En este punto nuestra red ha mejorado, esta por encima del 0.7 de acc, pero todavía tenemos que mejorarla. Comenzamos a introducir parámetros en nuestras capas Convolution2D y vamos cambiando para ver cuales son los que mejor funcionan. Incluimos también una capa densa con activación ReLu antes de la otra capa densa que teníamos. También introducimos el parámetro validation_split en nuestro modelo para ver como evoluciona en cada época, si hay sobreajuste, ….

Con esto llegamos al modelo con una accuracy por encima del 0.9. Este modelo ya es aceptable, y lo dejamos como modelo simple.

# Diseño de nuestro modelo
model = Sequential()

model.add(Conv2D(filters=32, kernel_size=(3,3), activation='relu', padding='valid', input_shape=(64, 64, 3), kernel_initializer = 'glorot_uniform', 
                 bias_initializer='zeros'))
model.add(MaxPooling2D(2,2))
model.add(Conv2D(filters=64, kernel_size=(3,3), activation='relu', padding='valid', kernel_initializer = 'glorot_uniform', bias_initializer='zeros'))
model.add(MaxPooling2D(2,2))
model.add(Conv2D(filters=128, kernel_size=(3,3), activation='relu', padding='valid', kernel_initializer = 'glorot_uniform', bias_initializer='zeros'))
model.add(Dropout(0.2))
model.add(MaxPooling2D(2,2))
model.add(Conv2D(filters=256, kernel_size=(3,3), activation='relu', padding='valid', kernel_initializer = 'glorot_uniform', bias_initializer='zeros'))
model.add(Flatten())
model.add(Dropout(0.5))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 62, 62, 32)        896       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 31, 31, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 29, 29, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 64)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 12, 12, 128)       73856     
_________________________________________________________________
dropout (Dropout)            (None, 12, 12, 128)       0         
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 6, 6, 128)         0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 4, 4, 256)         295168    
_________________________________________________________________
flatten (Flatten)            (None, 4096)              0         
_________________________________________________________________
dropout_1 (Dropout)          (None, 4096)              0         
_________________________________________________________________
dense (Dense)                (None, 512)               2097664   
_________________________________________________________________
dense_1 (Dense)              (None, 10)                5130      
=================================================================
Total params: 2,491,210
Trainable params: 2,491,210
Non-trainable params: 0
_________________________________________________________________

A modo de resumen tenemos lo siguiente:

• Crearemos varias capas de neuronas “Convolucional de 2 Dimensiones” Conv2D() , donde entrarán nuestras imágenes. Aplicaremos filtros (kernel) de tamaño 3×3 los cuales irán duplicando su número en cada capa. Estos filtros detectarán ciertas características de la imagen (ejemplo: lineas verticales). Además, utilizaremos La función ReLU como activación de las neuronas.

• Haremos un MaxPooling (de 2×2) que reduce la imagen que entra a la mitad,(11×14) manteniendo las características “únicas” que detectó cada kernel.

• Para evitar el overfitting, añadimos una técnica llamada Dropout.

• “Aplanamos” con Flatten() los 256 filtros y creamos una capa de 256 neuronas “tradicionales” Dense()

• Y finalizamos la capa de salida con 10 neuronas con activación Softmax, para que se corresponda con el “hot encoding” que hicimos antes.

• Luego compilamos nuestra red model.compile() y le asignamos un optimizador (en este caso de llama “Adam”). Como métrica utilizaremos “accuracy”.

# Compilamos, entrenamos y testamos
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=["accuracy"])
history = model.fit(
    X_train, 
    train_Y_one_hot, 
    batch_size=128, 
    validation_split=0.2,
    epochs=30, 
    verbose=2)

score = model.evaluate(X_test, test_Y_one_hot)
print("Test loss", score[0])
print("Test accuracy", score[1])

Epoch 1/30
3/3 - 0s - loss: 2.3607 - accuracy: 0.1073 - val_loss: 2.2406 - val_accuracy: 0.1061
Epoch 2/30
3/3 - 0s - loss: 2.2655 - accuracy: 0.1648 - val_loss: 2.2365 - val_accuracy: 0.1667
Epoch 3/30
3/3 - 0s - loss: 2.2259 - accuracy: 0.1609 - val_loss: 2.2199 - val_accuracy: 0.1515
Epoch 4/30
3/3 - 0s - loss: 2.1727 - accuracy: 0.1801 - val_loss: 2.1783 - val_accuracy: 0.1212
Epoch 5/30
3/3 - 0s - loss: 2.1124 - accuracy: 0.2069 - val_loss: 2.0665 - val_accuracy: 0.1364
Epoch 6/30
3/3 - 0s - loss: 1.9142 - accuracy: 0.3142 - val_loss: 2.0633 - val_accuracy: 0.2576
Epoch 7/30
3/3 - 0s - loss: 1.8644 - accuracy: 0.2605 - val_loss: 2.0834 - val_accuracy: 0.2273
Epoch 8/30
3/3 - 0s - loss: 1.7974 - accuracy: 0.3257 - val_loss: 1.8131 - val_accuracy: 0.3030
Epoch 9/30
3/3 - 0s - loss: 1.7962 - accuracy: 0.2644 - val_loss: 1.6129 - val_accuracy: 0.4091
Epoch 10/30
3/3 - 0s - loss: 1.4489 - accuracy: 0.4138 - val_loss: 1.5366 - val_accuracy: 0.3636
Epoch 11/30
3/3 - 0s - loss: 1.3547 - accuracy: 0.4406 - val_loss: 1.2228 - val_accuracy: 0.7273
Epoch 12/30
3/3 - 0s - loss: 1.0030 - accuracy: 0.7126 - val_loss: 1.0480 - val_accuracy: 0.6212
Epoch 13/30
3/3 - 0s - loss: 0.8564 - accuracy: 0.6552 - val_loss: 0.8582 - val_accuracy: 0.7576
Epoch 14/30
3/3 - 0s - loss: 0.6481 - accuracy: 0.8084 - val_loss: 0.8814 - val_accuracy: 0.6515
Epoch 15/30
3/3 - 0s - loss: 0.6478 - accuracy: 0.7778 - val_loss: 0.6642 - val_accuracy: 0.7273
Epoch 16/30
3/3 - 0s - loss: 0.3698 - accuracy: 0.8621 - val_loss: 0.5466 - val_accuracy: 0.7879
Epoch 17/30
3/3 - 0s - loss: 0.4609 - accuracy: 0.8161 - val_loss: 0.5240 - val_accuracy: 0.8939
Epoch 18/30
3/3 - 0s - loss: 0.3481 - accuracy: 0.8966 - val_loss: 0.5235 - val_accuracy: 0.8485
Epoch 19/30
3/3 - 0s - loss: 0.2911 - accuracy: 0.9004 - val_loss: 0.4273 - val_accuracy: 0.8788
Epoch 20/30
3/3 - 0s - loss: 0.2048 - accuracy: 0.9540 - val_loss: 0.3019 - val_accuracy: 0.9242
Epoch 21/30
3/3 - 0s - loss: 0.1657 - accuracy: 0.9540 - val_loss: 0.2679 - val_accuracy: 0.9545
Epoch 22/30
3/3 - 0s - loss: 0.1277 - accuracy: 0.9617 - val_loss: 0.3388 - val_accuracy: 0.8939
Epoch 23/30
3/3 - 0s - loss: 0.1136 - accuracy: 0.9693 - val_loss: 0.2268 - val_accuracy: 0.9697
Epoch 24/30
3/3 - 0s - loss: 0.0651 - accuracy: 0.9885 - val_loss: 0.2125 - val_accuracy: 0.9697
Epoch 25/30
3/3 - 0s - loss: 0.0566 - accuracy: 0.9847 - val_loss: 0.2045 - val_accuracy: 0.9697
Epoch 26/30
3/3 - 0s - loss: 0.0515 - accuracy: 0.9770 - val_loss: 0.1448 - val_accuracy: 0.9697
Epoch 27/30
3/3 - 0s - loss: 0.0446 - accuracy: 0.9847 - val_loss: 0.1798 - val_accuracy: 0.9697
Epoch 28/30
3/3 - 0s - loss: 0.0457 - accuracy: 0.9923 - val_loss: 0.2045 - val_accuracy: 0.9697
Epoch 29/30
3/3 - 0s - loss: 0.0292 - accuracy: 0.9923 - val_loss: 0.2337 - val_accuracy: 0.9697
Epoch 30/30
3/3 - 0s - loss: 0.0265 - accuracy: 0.9962 - val_loss: 0.3689 - val_accuracy: 0.9242
4/4 [==============================] - 0s 10ms/step - loss: 0.2076 - accuracy: 0.9541
Test loss 0.20761528611183167
Test accuracy 0.9541284441947937

Vemos como nuestro modelo con el conjunto de test tiene un “accuracy” por encima del 0.95% y una función de pérdida relativamente pequeña.

# guardamos la red, para reutilizarla en el futuro, sin tener que volver a entrenar
model.save("modelmahjong.h5py")

# Cargamos de nuevo nuestro modelo
model = load_model("modelmahjong.h5py")

import matplotlib.pyplot as plt
%matplotlib inline

# Vamos a revisar visualmente como funciona nuestro modelo para ver si podemos mejorarlo.
acc      = history.history[ 'accuracy' ]
val_acc  = history.history[ 'val_accuracy' ]
loss     = history.history[    'loss' ]
val_loss = history.history['val_loss' ]

epochs   = range(1,len(acc)+1,1)

plt.plot ( epochs,     acc, 'r--', label='Training acc'  )
plt.plot ( epochs, val_acc,  'b', label='Validation acc')
plt.title ('Training and validation accuracy')
plt.ylabel('acc')
plt.xlabel('epochs')

plt.legend()
plt.figure()

plt.plot ( epochs,     loss, 'r--' )
plt.plot ( epochs, val_loss ,  'b' )
plt.title ('Training and validation loss'   )
plt.ylabel('acc')
plt.xlabel('epochs')

plt.legend()
plt.figure()

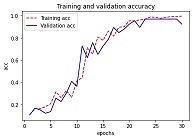
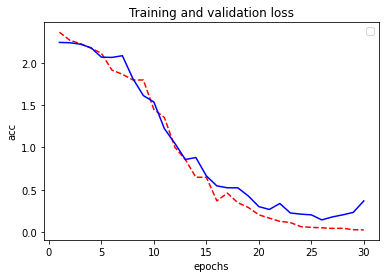
Visualmente podemos ver la accuracy no crece desde la época 23 aproximadamente, y la función de pérdida tiene su mínimo en la época 26. Con esto podemos concluir que nuestro modelo sobreajusta un poco. Para la versión más avanzada de nuestro modelo utilizaremos técnicas para no tener sobre ajuste con el early stopping de keras.

# Vamos a ver las imágenes en las que falla nuestro modelo:
preds = np.argmax(model.predict(X_test), axis=-1)
preds_one_hot = to_categorical(preds)
fails=np.where(test_Y_one_hot != preds_one_hot)
fails = set(fails[0])
print(fails)

{5, 72, 80, 92, 95}

# Vamos a ver unas cuantas imágenes a ver si visualmente detectamos donde esta el error:
for i in fails:
  print(i)
  print("Real Class", y_test[(i)], "predicted class", preds[i])
  n = plt.imshow(X_test[i])
  plt.show(n)

5
Real Class 8 predicted class 6

72
Real Class 8 predicted class 4

80
Real Class 8 predicted class 6

92
Real Class 8 predicted class 4

95
Real Class 8 predicted class 4

Como hay imágenes repetidas vemos que los fallos realmente han sido solo en 2 imágenes. Además, como comentábamos antes, las fichas en las que fallan son aquellas que tienen la insignia con el número, por lo que nos da una pista de donde pueden venir los errores.

Con esto finalizamos nuestra Red Neuronal Convolucional básica. Los siguiente pasos serán:

• Buscar un volumen importante de imágenes, como 50 por ficha creo sería suficiente.
• Utilizar Data Augmentation para crear un mayor número de imágenes.
• Utilizar las 34 imágenes que tiene un set de mahjong. Como dijimos las ruedas son las fichas más fáciles de reconocer, probablemente en nuestro modelo baje la accuracy.
• Utilizaremos los Call Backs de Keras para evitar el sobreajuste.
• Utilizaremos la técnica Grad Cam para analizar como funciona nuestro modelo e intentar ajustar los parámetros.