El Juego de la Vida: Programando en Python
El Juego de la vida es un autómata celular diseñado por el matemático británico John Horton Conway en 1970.
Se trata de un juego de cero jugadores, lo que quiere decir que su evolución está determinada por el estado inicial y no necesita ninguna entrada de datos posterior. El “tablero de juego” es una malla plana formada por cuadrados (las “células”) que se extiende por el infinito en todas las direcciones. Por tanto, cada célula tiene 8 células “vecinas”, que son las que están próximas a ella, incluidas las diagonales. Las células tienen dos estados: están “vivas” o “muertas”. El estado de las células evoluciona a lo largo de unidades de tiempo discretas (se podría decir que por momentos). El estado de todas las células se tiene en cuenta para calcular el estado de las mismas en el siguiente momento. Todas las células se actualizan simultáneamente en cada turno, siguiendo estas reglas:
Una célula muerta con exactamente 3 células vecinas vivas “nace” (es decir, al turno siguiente estará viva). Una célula viva con 2 o 3 células vecinas vivas sigue viva, en otro caso muere (por “soledad” o “superpoblación”).
Se puede encontrar más información en https://es.wikipedia.org/wiki/Juego_de_la_vida
En el blog vamos a ver como programarlo con Python. Vamos a ello:
1.Importamos librerías
En primer lugar instalamos las librerías necesarias: pygame y numpy. Pygame es una librería con muchas funcionalidades para crear juegos en python, y la librería numpy nos facilita el trabajo con matrices y funciones matemáticas:
# Importamos librerías:
import pygame
import numpy as np
2. Creamos la pantalla del juego
Iniciamos pygame:
pygame.init()
Le damos un alto y un ancho de 600 pixels.
width = 600
height = 600
screem = pygame.display.set_mode((height, width))
Y un color de fondo gris oscuro.
bg = 25, 25, 25
screem.fill(bg)
Al ejecutar este código se abriría la pantalla, pero se cerraría inmediatamente.
Para mantener la pantalla de manera indefinida, creamos un bucle infinito. Quedaría así.
import pygame
import numpy as np
pygame.init()
width = 600
height = 600
screem = pygame.display.set_mode((height, width))
bg = 25, 25, 25
screem.fill(bg)
while True:
pass
Con esto tenemos la pantalla sobre la que iremos trabajando.
2. Celdas
El siguiente paso es dividir la pantalla en celdas, para ello definiremos el numero de particiones horizontales y verticales que queremos realizar. Tras esto, dividirimos el alto y ancho de la pantalla entre esas particiones.
# Número de particiones o celdas
ncX, ncY = 50, 50
# Dimensiones de las celdas
dimCW = width / ncX
dimCH = height / ncY
Con esta división hemos definido las celdas que aparecerán en cada uno de los “momentos”. Para poder visualizarlas creamos 2 bucles que recorran cada una de las celdas que hemos generado en el eje X y en el eje Y.
Con la función draw.polygon dibujamos las celdas. Debemos incluir como parámetros la pantalla, el color, los puntos que definan el polígono que estamos dibujando*, y el ancho de 1 pixel.
*Los puntos quedarían así definidos:
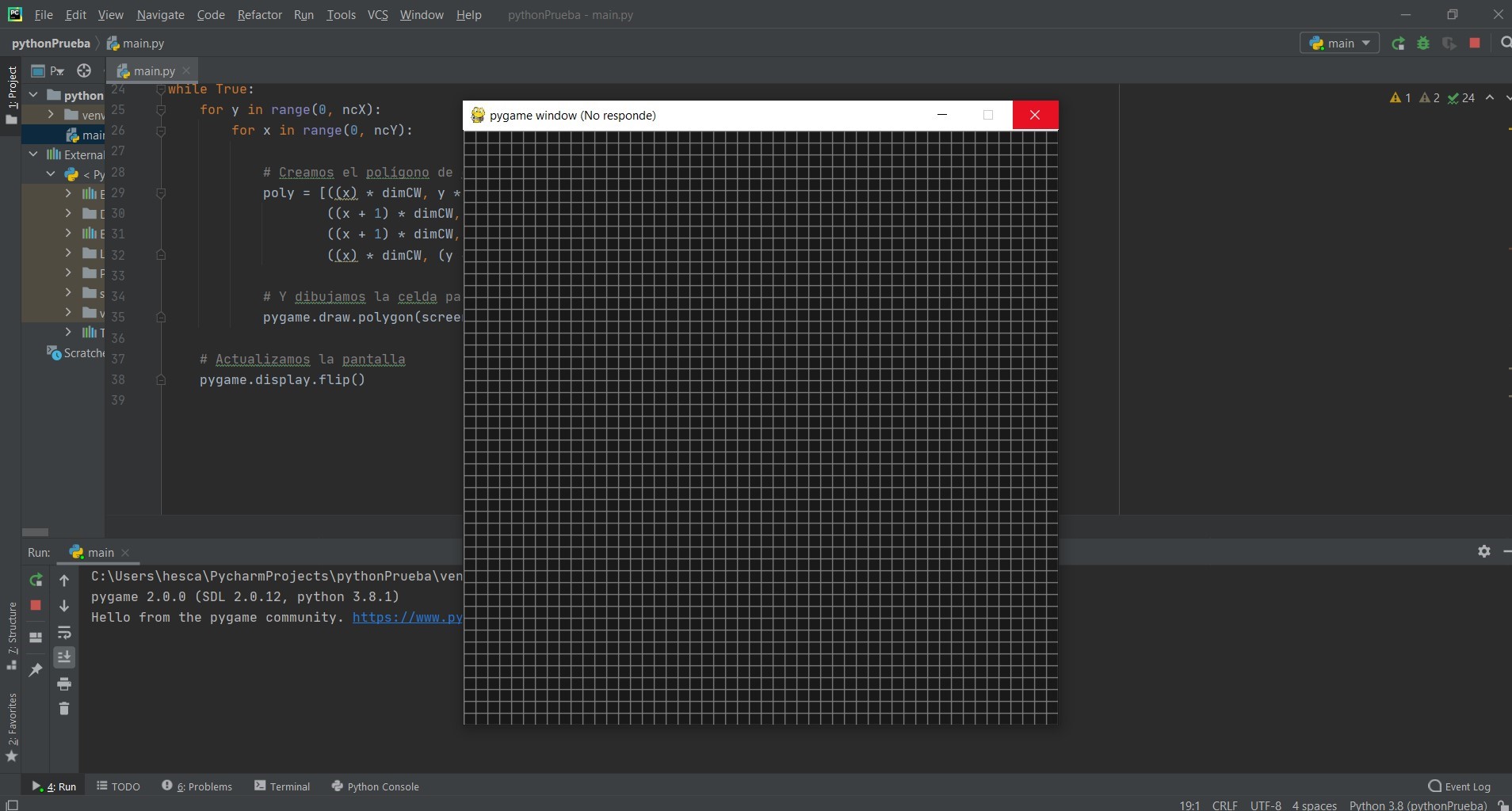
Y este sería el código.
for y in range(0, ncX):
for x in range(0, ncY):
poly = [((x) * dimCW, y * dimCH),
((x + 1) * dimCW, y * dimCH),
((x + 1) * dimCW, (y + 1) * dimCH),
((x) * dimCW, (y + 1) * dimCH)]
pygame.draw.polygon(screem, (128, 128, 128), poly, 1)
Con la función display mostramos las celdas en cada iteración del bucle.
pygame.display.flip()
Nuestro código quedaría así.
# Importamos las librerías necesarias:
import pygame
import numpy as np
# Para comenzar vamos a crear la pantalla de nuestro juego
pygame.init()
width = 600
height = 600
screem = pygame.display.set_mode((height, width))
bg = 25, 25, 25
screem.fill(bg)
# Número de celdas
ncX, ncY = 50, 50
# Dimensiones de las celdas
dimCW = width / ncX
dimCH = height / ncY
while True:
for y in range(0, ncX):
for x in range(0, ncY):
# Creamos el polígono de cada celda a dibujar
poly = [((x) * dimCW, y * dimCH),
((x + 1) * dimCW, y * dimCH),
((x + 1) * dimCW, (y + 1) * dimCH) ,
((x) * dimCW, (y + 1) * dimCH)]
# Y dibujamos la celda para cada par de X e Y.
pygame.draw.polygon(screem, (128, 128, 128), poly, 1)
# Actualizamos la pantalla
pygame.display.flip()
Y tendríamos así la pantalla.
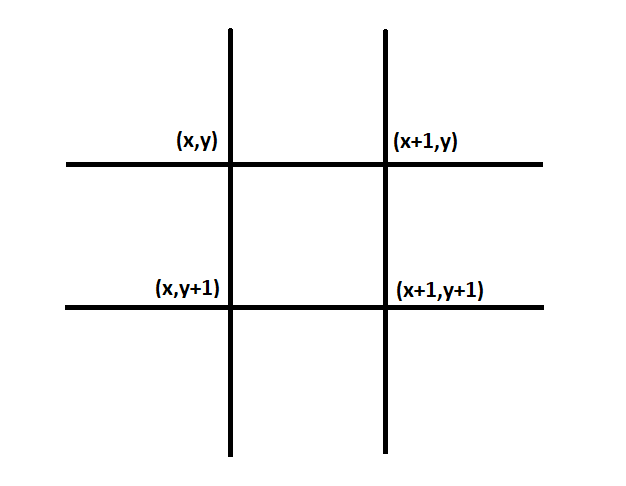
3. Estado de las Celdas
Ahora vamos a generar una estructura de datos que contenga el estado de cada celda. Las celdas pueden estar vivas cuando son iguales a 1, y muertas cuando son igual a 0.
Para esto vamos a crear una matriz de tamaño igual al número de celdas que tenemos, y que en un momento inicial este completamente a 0.
#Estado de las celdas. Vivas = 1; Muertas = 0
gameState = np.zeros((ncX, ncY))
Como hemos visto inicialmente con unas simples reglas podemos llegar a un comportamiento complejo. Estas reglas alteran el estado de cada celda en cada “momento”. Este cambio de estado va a depender del estado de las celdas vecinas (hay 8 celdas vecinas para cada celda) a la que estamos analizando.
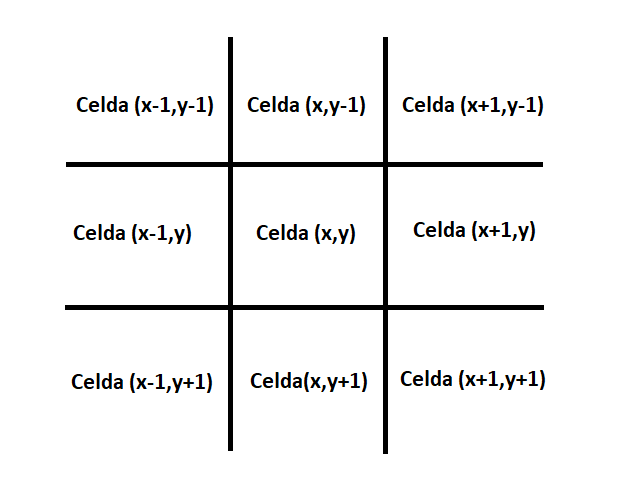
En el caso de las celdas que se encuentran en los bordes de nuestra pantalla de juego, las celdas vecinas van a ser las que se encuentran en el borde opuesto. Vamos a visualizar la pantalla como si fuera un toroide, es decir, la pantalla no termina en un borde sino que continua por el borde contrario. Para esto vamos a utilizar la operación módulo.
# Calculamos el número de vecinos cercanos que están vivos, ya que esto es lo que hará cambiar el estado de las celdas.
# Lo veremos en detalle con las reglas.
n_neigh = gameState[(x-1) % ncX, (y-1) % ncY] + \
gameState[(x) % ncX, (y-1) % ncY] + \
gameState[(x+1) % ncX, (y-1) % ncY] + \
gameState[(x-1) % ncX, (y) % ncY] + \
gameState[(x+1) % ncX, (y) % ncY] + \
gameState[(x-1) % ncX, (y+1) % ncY] + \
gameState[(x) % ncX, (y+1) % ncY] + \
gameState[(x+1) % ncX, (y+1) % ncY]
4. Reglas
Con dos simples reglas vamos a definir el comportamiento de nuestras celdas:
- Si una celda muerta tiene exactamente 3 celdas vecinas vivas (n_neigh = 3) su estado pasa a estar viva.
- Si una celda viva tiene menos de 2 o más de 3 celdas vecinas vivas muere (3 < n_neigh < 2).
# Rule 1: Una celda muerta con exactamente 3 vecinas vivas, "revive".
if gameState[x, y] == 0 and n_neigh == 3:
gameState[x, y] = 1
# Rule 2: Una celda viva con menos de 2 o más de 3 celdas vivas alrededor muere.
elif gameState[x, y] == 1 and (n_neigh < 2 or n_neigh > 3):
gameState[x, y] = 0
Con las reglas que hemos incluido ya conseguiríamos cambiar el estado de las celdas en cada iteración. El problema es que este cambio se produce de manera secuencial y en el mismo “momento” una celda que haya cambiado de estado afectaría al estado de las siguientes. Esto no debería ser así y deberían cambiar de estado todas en el mismo “momento”.
Para solucionar esto, en cada iteración debemos realizar una copia del estado inicial, y los cambios en el estado de las celdas deben ser reflejados en esta copia.
# Creamos un copia del gameState sobre la que haremos los cambios,para que se realicen a la vez en cada "momento"
newGameState = np.copy(gameState)
# Y modificamos las reglas.
if gameState[x, y] == 0 and n_neigh == 3:
newGameState[x, y] = 1
elif gameState[x, y] == 1 and (n_neigh < 2 or n_neigh > 3):
newGameState[x, y] = 0
# Al final de bucle actualizaremos el estado de todas las celdas al mismo tiempo.
gameState = np.copy(newGameState)
Además, debemos rellenar del color adecuado (*celdas vivas de color blanco, y las muertas se quedan en negro)
# Rellenamos de color cada celda para cada par de X e Y.
if newGameState[x, y] == 0:
pygame.draw.polygon(screem, (128, 128, 128), poly, 1)
else:
pygame.draw.polygon(screem, (255, 255, 255), poly, 0)
Nuestro código en este punto es el siguiente.
# Importamos las librerías necesarias:
import pygame
import numpy as np
# Para comenzar vamos a crear la pantalla de nuestro juego
pygame.init()
width = 600
height = 600
screem = pygame.display.set_mode((height, width))
bg = 25, 25, 25
screem.fill(bg)
# Número de celdas
ncX, ncY = 50, 50
# Dimensiones de las celdas
dimCW = width / ncX
dimCH = height / ncY
# Estado de las celdas. Vivas = 1; Muertas = 0
gameState = np.zeros((ncX, ncY))
# Vamos a inlcuir alguna celda viva en el inicio para ver su comportamiento
gameState[21,21] = 1
gameState[22,22] = 1
gameState[22,23] = 1
gameState[21,23] = 1
gameState[20,23] = 1
while True:
# Creamos un copia del gameState sobre la que haremos los cambios, para que se realicen a la vez en cada momento
newGameState = np.copy(gameState)
for y in range(0, ncX):
for x in range(0, ncY):
# Calculamos el número de vecinos cercanos
n_neigh = gameState[(x - 1) % ncX, (y - 1) % ncY] + \
gameState[(x) % ncX, (y - 1) % ncY] + \
gameState[(x + 1) % ncX, (y - 1) % ncY] + \
gameState[(x - 1) % ncX, (y) % ncY] + \
gameState[(x + 1) % ncX, (y) % ncY] + \
gameState[(x - 1) % ncX, (y + 1) % ncY] + \
gameState[(x) % ncX, (y + 1) % ncY] + \
gameState[(x + 1) % ncX, (y + 1) % ncY]
# Rule 1: Una celda muerta con exactamente 3 vecinas vivas, "revive".
if gameState[x, y] == 0 and n_neigh == 3:
newGameState[x, y] = 1
# Rule 2: Una celda viva con menos de 2 o más de 3 celdas vivas alrededor muere.
elif gameState[x, y] == 1 and (n_neigh < 2 or n_neigh > 3):
newGameState[x, y] = 0
# Creamos el polígono de cada celda a dibujar
poly = [((x) * dimCW, y * dimCH),
((x + 1) * dimCW, y * dimCH),
((x + 1) * dimCW, (y + 1) * dimCH),
((x) * dimCW, (y + 1) * dimCH)]
# Y coloreamos la celda para cada par de X e Y.
if newGameState[x, y] == 0:
pygame.draw.polygon(screem, (128, 128, 128), poly, 1)
else:
pygame.draw.polygon(screem, (255, 255, 255), poly, 0)
# Al final de bucle actualizaremos el estado de todas las celdas al mismo tiempo.
gameState = np.copy(newGameState)
# Actualizamos la pantalla
pygame.display.flip()
Ya tenemos programado lo básico de nuestro juego, pero tiene algún fallo. Vemos como las celdas vivas se van superponiendo entre cada uno de nuestros “momentos”, por lo que la pantalla se vuelve blanca según avanza el autómata. Lo que tenemos que hacer es borrar el estado de la pantalla entre cada momento.
# Coloreamos la pantalla totalmente de gris cada vuelta.
screem.fill (bg)
Vamos a importar el módulo time, para usar la función time.sleep y que nuestro juego se pueda tomar entre cada “momento” un pequeño descanso.
import time
# Creamos un lapso de tiempo para que se aprecie mejor el movimiento
time.sleep(0.1)
Para finalizar vamos a incluir una serie de mejoras, que nos permitan para la ejecución, dara vida a las celdas, eliminar la vida de las celdas,…
Con esto quedaría nuestro código definitivo así:
# Importamos las librerías necesarias:
import pygame
import numpy as np
import time
# Para comenzar vamos a crear la pantalla de nuestro juego
pygame.init()
width = 600
height = 600
screem = pygame.display.set_mode((height, width))
bg = 25, 25, 25
screem.fill(bg)
# Número de celdas
ncX, ncY = 50, 50
# Dimensiones de las celdas
dimCW = width / ncX
dimCH = height / ncY
#Estado de las celdas. Vivas = 1; Muertas = 0
gameState = np.zeros((ncX, ncY))
# Autómata andar
gameState[21, 21] = 1
gameState[22, 22] = 1
gameState[22, 23] = 1
gameState[21, 23] = 1
gameState[20, 23] = 1
# Control de la ejecución del juego
pauseExect = False
# Bucle de ejecución
while True:
# Creamos un copia del gameState sobre la que haremos los cambios,
# para que se realicen a la vez en cada vuelta del bucle
newGameState = np.copy(gameState)
# Coloreamos la pantalla totalmente de gris cada vuelta.
screem.fill (bg)
# Creamos un lapso de tiempo para que se aprecie mejor el movimiento
time.sleep(0.1)
# Registramos eventos del teclado y ratón
ev = pygame.event.get()
for event in ev:
# Detectamos si se presiona una tecla
if event.type == pygame.KEYDOWN:
pauseExect = not pauseExect
# Detectamos si se presiona el ratón
mouseClick = pygame.mouse.get_pressed()
if sum(mouseClick) > 0:
posX, posY = pygame.mouse.get_pos()
celX, celY = int(np.floor(posX / dimCW)), int(np.floor(posY / dimCH))
newGameState[celX, celY] = 1
for y in range(0, ncX):
for x in range(0, ncY):
if not pauseExect:
# Calculamos el número de vecinos cercanos
n_neigh = gameState[(x-1) % ncX, (y-1) % ncY] + \
gameState[(x) % ncX, (y-1) % ncY] + \
gameState[(x+1) % ncX, (y-1) % ncY] + \
gameState[(x-1) % ncX, (y) % ncY] + \
gameState[(x+1) % ncX, (y) % ncY] + \
gameState[(x-1) % ncX, (y+1) % ncY] + \
gameState[(x) % ncX, (y+1) % ncY] + \
gameState[(x+1) % ncX, (y+1) % ncY]
# Rule 1: Una celda muerta con exactamente 3 vecinas vivas, "revive".
if gameState[x, y] == 0 and n_neigh == 3:
newGameState[x, y] = 1
# Rule 2: Una celda viva con menos de 2 o más de 3 celdas vivas alrededor muere.
elif gameState[x, y] == 1 and (n_neigh < 2 or n_neigh > 3):
newGameState[x, y] = 0
# Creamos el polígono de cada celda a dibujar
poly = [((x) * dimCW, y * dimCH),
((x + 1) * dimCW, y * dimCH),
((x + 1) * dimCW, (y + 1) * dimCH),
((x) * dimCW, (y + 1) * dimCH)]
# Y dibujamos la celda para cada par de X e Y.
if newGameState[x, y] == 0:
pygame.draw.polygon(screem, (128, 128, 128), poly, 1)
else:
pygame.draw.polygon(screem, (255, 255, 255), poly, 0)
# Actualizamos el estado del juegos
gameState = np.copy(newGameState)
# Actualizamos la pantalla
pygame.display.flip()
Por último quiero agradecer al canal de Youtube Dot CSV (https://www.youtube.com/channel/UCy5znSnfMsDwaLlROnZ7Qbg) del cual he podido aprender a programar este juego de la vida.
