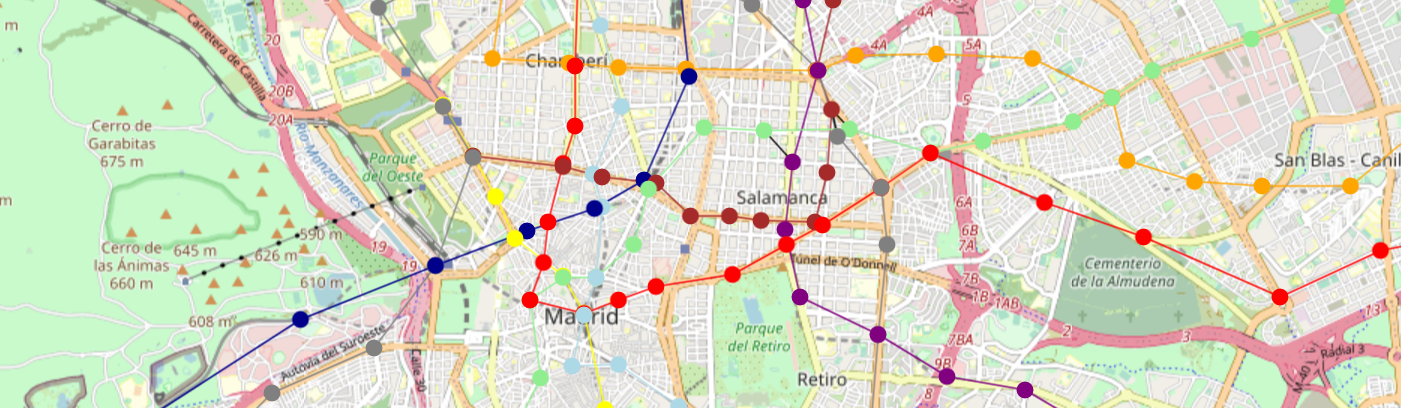
Grafo Red de Metro de Madrid con librería NetworkX
¿Qué es un grafo?
Los grafos son una estructura de datos que permiten modelar la información visualmente. Estas estructuras aportan mucho valor tanto en áreas científicas (biología, sociología, …), como en áreas de negocio (estudios de mercado, detección de fraude, …). Debido a la gran cantidad de aplicaciones en la optimización de recorridos, procesos, flujos y algoritmos de búsquedas entre otros, se ha generado toda una nueva teoría que se conoce como análisis de redes.
Matemáticamente, un grafo es un par ordenado G = ( V , A) donde V es un conjunto no vacío de vértices (o nodos) y A un conjunto de aristas que relacionan elementos (vértices) entre sí. Gráficamente se representan como círculos (que son los vértices) unidos por líneas (que son las aristas). Mediante los grafos podemos describir multitud de procesos, situaciones, relaciones, estructuras, etc.

Hay situaciones en las que nos interesa especificar que una relación (arista) tiene una dirección concreta. Un simil de esto sería la red de tuberías de una ciudad en la que el agua solo puede circular en una dirección. Este tipo de grafos se llaman digrafos o grafos dirigidos.
Las aristas, además de ser dirigidas, pueden tener un valor o un peso que aporta cierta información acerca de las relaciones. Son los llamados grafos ponderados. Volviendo a nuestro simil, podríamos tener la cantidad de agua de circula por cada tubería (vértice).
Según estas características podemos dividir los grafos por tipos.
Tipos de grafos:
- Grafo simple: O simplemente grafo es aquel que acepta una sola arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un grafo.
- Multigrafo o pseudografo: Es el que acepta más de una arista entre dos vértices. Estas aristas se llaman múltiples o lazos (loops en inglés). Los grafos simples son una subclase de esta categoría de grafos. También se les llama grafos general.
- Grafo orientado: grafo dirigido o dígrafo. Son grafos en los cuales se ha añadido una orientación a las aristas, representada gráficamente por una flecha.
- Grafo etiquetado: Grafos en los cuales se ha añadido un peso a las aristas (número entero generalmente) o un etiquetado a los vértices.
- Grafo aleatorio: Grafo cuyas aristas están asociadas a una probabilidad.
- Hipergrafo: Grafos en los cuales las aristas tienen más de dos extremos, es decir, las aristas son incidentes a 3 o más vértices.
- Grafo infinito: Grafos con conjunto de vértices y aristas de cardinal infinito.
- Grafo plano: Los grafos planos son aquellos cuyos vértices y aristas pueden ser representados sin ninguna intersección entre ellos. Podemos establecer que un grafo es plano gracias al Teorema de Kuratowski.
- Grafo regular: Un grafo es regular cuando todos sus vértices tienen el mismo grado de valencia.
- Grafo dual: El grafo dual G´ de un grafo G (plano), es aquel que tiene un vértice por cada región de G, y una arista por cada arista en G uniendo dos regiones vecinas.
Tras un pequeño resumen teórico, vamos a comenzar nuestro proyecto, que consiste en lo siguiente:
- Graficar el plano de Metro de Madrid con la librería NetworkX de python:
- Explicaremos en detalle su funcionamiento e iremos paso a paso creando nuestro grafo.
- Geolocalizaremos las estaciones, y los tramos.
- Graficaremos el resultado sobre un mapa.
- Explicaremos algoritmos de centralidad y los aplicaremos a nuestro grafo.
- Utilizaremos el algoritmo Dijkstra para hayar la ruta más corta entre 2 estaciones.
Comenzamos nuestro proyecto
#Cargamos las librerías necesarias
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx # librería de grafos
import mplleaflet # Visualización sobre mapas
import warnings
warnings.filterwarnings('ignore') # Ignora warnings
# pd.set_option('display.max_rows', None) # Para ver los dataframes completos
Para nuestro ejercicio contamos con dos datasets, estaciones y tramos. Estos datos han sido obtenidos del portal de Datos Abiertos del Consorcio Regional de Transporte de Madrid (https://data-crtm.opendata.arcgis.com/) y posteriormente manipulados para reflejar la información que nos interesa en nuestro proyecto.
0. Carga de datos
Estaciones:
- id: identificador único de la estación.
- estación: nombre de la estación (una estación por la que pasan varias líneas tendrá varios registros).
- línea: línea a la que pertenece la estación.
- transbordo: en caso afirmativo son estaciones por las que pasan varias líneas de metro (no de otro medio de transporte).
- lat y long: se ha añadido la latitud y longitud para ubicarlas en el mapa.
- estacion_linea: unión de las columnas estación y línea para poder identificar la estación de la línea adecuada, y así poder graficar mejor.
# Cargamos Estaciones
estaciones = pd.read_excel('Estaciones.xlsx')
estaciones
| id | estacion | linea | transbordo | lat | long | estacion_linea | |
|---|---|---|---|---|---|---|---|
| 0 | 2 | ABRANTES | 11 | NO | 40.380827 | -3.727911 | ABRANTES_11 |
| 1 | 21 | ACACIAS | 5 | SI | 40.403869 | -3.706652 | ACACIAS_5 |
| 2 | 6 | AEROPUERTO T1 T2 T3 | 8 | NO | 40.468644 | -3.569541 | AEROPUERTO T1 T2 T3_8 |
| 3 | 8 | AEROPUERTO T4 | 8 | NO | 40.491759 | -3.593254 | AEROPUERTO T4_8 |
| 4 | 1 | ALAMEDA DE OSUNA | 5 | NO | 40.457788 | -3.587530 | ALAMEDA DE OSUNA_5 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 282 | 29 | VILLA DE VALLECAS | 1 | NO | 40.379593 | -3.621308 | VILLA DE VALLECAS_1 |
| 283 | 18 | VILLAVERDE ALTO | 3 | NO | 40.341223 | -3.711991 | VILLAVERDE ALTO_3 |
| 284 | 16 | VILLAVERDE BAJO CRUCE | 3 | NO | 40.350890 | -3.692651 | VILLAVERDE BAJO CRUCE_3 |
| 285 | 18 | VINATEROS | 9 | NO | 40.410240 | -3.652740 | VINATEROS_9 |
| 286 | 26 | VISTA ALEGRE | 5 | NO | 40.388842 | -3.739827 | VISTA ALEGRE_5 |
287 rows × 7 columns
Tramos:
- origen: estación de origen
- destino: estación destino
- segundos: tiempo en segundos, según el portal de Datos Abierto.
- origen_linea y destino_linea: igual que origen y destino con la estacion_linea
# Cargamos Tramos
tramos = pd.read_csv('tramosEstacionesTrasbordos.csv', ';')
tramos
| origen | destino | segundos | origen_linea | destino_linea | |
|---|---|---|---|---|---|
| 0 | ABRANTES | PAN BENDITO | 106 | ABRANTES_11 | PAN BENDITO_11 |
| 1 | ACACIAS | PIRAMIDES | 85 | ACACIAS_5 | PIRAMIDES_5 |
| 2 | AEROPUERTO T1 T2 T3 | BARAJAS | 119 | AEROPUERTO T1 T2 T3_8 | BARAJAS_8 |
| 3 | ALAMEDA DE OSUNA | EL CAPRICHO | 113 | ALAMEDA DE OSUNA_5 | EL CAPRICHO_5 |
| 4 | ALCORCON CENTRAL | PARQUE OESTE | 139 | ALCORCON CENTRAL_12 | PARQUE OESTE_12 |
| ... | ... | ... | ... | ... | ... |
| 322 | VILLA DE VALLECAS | CONGOSTO | 126 | VILLA DE VALLECAS_1 | CONGOSTO_1 |
| 323 | VILLAVERDE ALTO | SAN CRISTOBAL | 235 | VILLAVERDE ALTO_3 | SAN CRISTOBAL_3 |
| 324 | VILLAVERDE BAJO CRUCE | CIUDAD DE LOS ANGELES | 142 | VILLAVERDE BAJO CRUCE_3 | CIUDAD DE LOS ANGELES_3 |
| 325 | VINATEROS | ARTILLEROS | 115 | VINATEROS_9 | ARTILLEROS_9 |
| 326 | VISTA ALEGRE | CARABANCHEL | 96 | VISTA ALEGRE_5 | CARABANCHEL_5 |
327 rows × 5 columns
A los transbordos les hemos dado un coste inicial en segundos de 120.
1. Graficar el plano de Metro de Madrid
Para comenzar vamos a almacenar cierta información en un diccionario y a crear un par de funciones que nos harán falta más adelante
Creamos un diccionario con las líneas y las estaciones que las componen.
# Creamos un lista con las líneas
lineas = sorted(estaciones['linea'].unique())
# Creamos un diccionario vacío
estaciones_linea = {}
# Con un bucle cargamos los datos en el diccionario
for li in lineas:
estaciones_linea['linea' + str(li)] = estaciones['estacion_linea'].values[estaciones['linea'] == li]
#Comprobamos
estaciones_linea['linea1']
array(['ALTO DEL ARENAL_1', 'ALVARADO_1', 'ANTON MARTIN_1', 'ATOCHA_1',
'ATOCHA RENFE_1', 'BAMBU_1', 'BILBAO_1', 'BUENOS AIRES_1',
'CHAMARTIN_1', 'CONGOSTO_1', 'CUATRO CAMINOS_1', 'ESTRECHO_1',
'GRAN VIA_1', 'IGLESIA_1', 'LA GAVIA_1', 'LAS SUERTES_1',
'MENENDEZ PELAYO_1', 'MIGUEL HERNANDEZ_1', 'NUEVA NUMANCIA_1',
'PACIFICO_1', 'PINAR DE CHAMARTIN_1', 'PLAZA DE CASTILLA_1',
'PORTAZGO_1', 'PUENTE DE VALLECAS_1', 'RIOS ROSAS_1',
'SIERRA DE GUADALUPE_1', 'SOL_1', 'TETUAN_1', 'TIRSO DE MOLINA_1',
'TRIBUNAL_1', 'VALDEACEDERAS_1', 'VALDECARROS_1',
'VILLA DE VALLECAS_1'], dtype=object)
Ahora vamos a crear dos funciones (de una manera muy artesanal) para poder colorear tanto los nodos como los tramos, y así visualizar el plano de metro más real.
Los transbordos los pintaremos en negro.
#Función para colorear los nodos
def colorear_nodos(G):
color = []
for node in G.nodes:
if node in estaciones_linea['linea1']:
color.append('lightblue')
elif node in estaciones_linea['linea2']:
color.append('red')
elif node in estaciones_linea['linea3']:
color.append('yellow')
elif node in estaciones_linea['linea4']:
color.append('brown')
elif node in estaciones_linea['linea5']:
color.append('lightgreen')
elif node in estaciones_linea['linea6']:
color.append('gray')
elif node in estaciones_linea['linea7']:
color.append('orange')
elif node in estaciones_linea['linea8']:
color.append('pink')
elif node in estaciones_linea['linea9']:
color.append('purple')
elif node in estaciones_linea['linea10']:
color.append('darkblue')
elif node in estaciones_linea['linea11']:
color.append('darkgreen')
elif node in estaciones_linea['linea12']:
color.append('gold')
else:
color.append('black')
return color
#Función para colorear los vértices
def colorear_edges(G):
color_edge = []
for edge in G.edges:
if edge[1] in estaciones_linea['linea1'] and edge[0] in estaciones_linea['linea1']:
color_edge.append('lightblue')
elif edge[1] in estaciones_linea['linea2'] and edge[0] in estaciones_linea['linea2']:
color_edge.append('red')
elif edge[1] in estaciones_linea['linea3'] and edge[0] in estaciones_linea['linea3']:
color_edge.append('yellow')
elif edge[1] in estaciones_linea['linea4'] and edge[0] in estaciones_linea['linea4']:
color_edge.append('brown')
elif edge[1] in estaciones_linea['linea5'] and edge[0] in estaciones_linea['linea5']:
color_edge.append('lightgreen')
elif edge[1] in estaciones_linea['linea6'] and edge[0] in estaciones_linea['linea6']:
color_edge.append('gray')
elif edge[1] in estaciones_linea['linea7'] and edge[0] in estaciones_linea['linea7']:
color_edge.append('orange')
elif edge[1] in estaciones_linea['linea8'] and edge[0] in estaciones_linea['linea8']:
color_edge.append('pink')
elif edge[1] in estaciones_linea['linea9'] and edge[0] in estaciones_linea['linea9']:
color_edge.append('purple')
elif edge[1] in estaciones_linea['linea10'] and edge[0] in estaciones_linea['linea10']:
color_edge.append('darkblue')
elif edge[1] in estaciones_linea['linea11'] and edge[0] in estaciones_linea['linea11']:
color_edge.append('darkgreen')
elif edge[1] in estaciones_linea['linea12'] and edge[0] in estaciones_linea['linea12']:
color_edge.append('gold')
else:
color_edge.append('black')
return color_edge
Con esto ya estamos listos para construir nuestro Grafo. Ahora los pasos a seguir son los siguientes:
- Creación del Grafo (Puede ser dirigido o No dirigido).
- Añadimos Nodos (en este caso no vamos a añadir los nodos, ya que al añadir las aristas y la posición de los nodos no es necesario).
- Añadimos aristas.
- Definición de la posición de los nodos(en nuestro caso es importante ya que tenemos geolocalizados los nodos. En otros casos no será importante, y podemos dejar que se ubique aleatoriamente o con una distribución concreta. Puedes ver más infomación en https://networkx.org/).
- Definimos y asignamos atributos al grafo.
- Graficamos.
# 1. Creación del grafo
G = nx.Graph()
# En nuestro caso es un grafo no dirigido ya que las relaciones entre las estaciones son bidireccionales.
# Para crear un grafo dirigido -> G = nx.DiGraph()
# 2. Añadimos nodos
# Como hemos mencionado anteriormente no vamos a añadir los nodos directamente, ya que al añadir las aristas
# y la posición no es necesario.
# Para añadir nodos -> G.add_nodes(único nodo, atributos) o G.add_nodes_from(lista de nodos, lista atributos)
# 3. Añadimos aristas
# Si quisieramos incluir información en las aristas, crearíamos un diccionario
# edge_labels = {}
# Introducimos origen, destino y peso (coste en segundos) de nuestras aristas
for origen, destino, segundos in zip(tramos['origen_linea'], tramos['destino_linea'], tramos['segundos']):
G.add_edge(origen, destino, weight = segundos)
# Podríamos incluir información en las etiquetas de las aristas, por ejemplo los segundos
# edge_labels[(origen,destino)] = '{:,}'.format(int(segundos)).replace(',','.')
# 4. Definimos la posición que van a tener cada nodo y lo guardamos en un diccionario.
# Creamos diccionario vacío para las posiciones de los nodos
pos = {}
# Introducimos lat y long según el nodo
for i in range(0, len(estaciones)):
pos[estaciones.iloc[i, 6]] = (estaciones.iloc[i, 5], estaciones.iloc[i, 4])
# 5. Definimos atributos
# Color de nodos y aristas
color = colorear_nodos(G)
color_edge = colorear_edges(G)
# Definimos el tamaño de la imagen
fig, ax = plt.subplots(figsize = (20,10))
# Asignamos atributos al grafo
nx.draw(G,
pos = pos,
#with_labels = True, (Para activar las etiquetas de los nodos)
font_size = 10,
node_color = color,
node_size = 100,
edge_color = color_edge)
# Para visualizar las etiquetas de las aristas
# nx.draw_networkx_edge_labels(G,
# pos,
# edge_labels = edge_labels,
# font_size = 17)
# 6. Graficamos
# Vamos a graficar con la librería mplleaflet, para poder observar sobre un mapa nuestro grafo.
mplleaflet.display(fig=ax.figure)
# Si no quieres que aparezca sobre un mapa, puedes utilizar
#plt.show()
Agrupando los 6 pasos tenemos lo siguiente
# Definimos el grafo no dirigido
G = nx.Graph()
# Añadimos las aristas, con los segundos que se tarda en cada tramo.
for origen, destino, segundos in zip(tramos['origen_linea'], tramos['destino_linea'], tramos['segundos']):
G.add_edge(origen, destino, weight = segundos)
# Definimos la posición que van a tener cada nodo y lo guardamos en un diccionario.
pos = {}
for i in range(0, len(estaciones)):
pos[estaciones.iloc[i, 6]] = (estaciones.iloc[i, 5], estaciones.iloc[i, 4])
# Definimos el tamaño de la imagen
fig, ax = plt.subplots(figsize = (20,10))
# Coloreamos nodos y aristas
color = colorear_nodos(G)
color_edge = colorear_edges(G)
# Asignamos atributos
nx.draw(G,
pos = pos,
node_color = color,
edge_color = color_edge,
font_size = 10,
node_size = 100)
# Vamos a graficar con la librería mplleaflet, para poder observar sobre un mapa nuestro grafo.
mplleaflet.display(fig=ax.figure)
2. Algoritmos de centralidad
Como hemos incluido estaciones repetidas con el fin de poder graficar los transbordos, vamos a crear otro grafo en el aparezca únicamente una vez cada estación. En este caso no es necesario definir atributos, ya que no vamos a graficar.
# Definimos el grafo
G2 = nx.Graph()
# Añadimos las aristas
for origen, destino in zip(tramos['origen'], tramos['destino']):
G2.add_edge(origen, destino)
Ahora vamos a ver algunos de los algoritmos de centralidad y cómo interpretarlos en nuestro grafo
Centralidad de grados
La centralidad de grado es una de las medidas más simples de centralidad.
Mide el número de enlaces o conexiones que tiene un nodo con los demás nodos pertenecientes a un grafo. Cuando se aplica un análisis de este tipo pueden determinarse diferentes medidas. Por ejemplo, en redes sociales podemos medir el grado de entrada de un nodo como la popularidad o preferencia que posea y la salida definirla como un indicador de sociabilidad.
En nuestro caso vamos a ver las estaciones más relacionadas, es decir, que tienen más aristas. Esto es debido a que pasa un mayor número de líneas por esa estación
# Centralidad de grados
pd.DataFrame.from_dict(nx.algorithms.centrality.degree_centrality(G2),
orient='index',
columns = ['grado_centralidad'])\
.sort_values(['grado_centralidad'],
ascending = False)\
.head(10)
| grado_centralidad | |
|---|---|
| AVENIDA DE AMERICA | 0.037500 |
| ALONSO MARTINEZ | 0.033333 |
| SOL | 0.033333 |
| NUEVOS MINISTERIOS | 0.029167 |
| DIEGO DE LEON | 0.029167 |
| CUATRO CAMINOS | 0.029167 |
| PLAZA DE CASTILLA | 0.029167 |
| SAN BERNARDO | 0.025000 |
| COLOMBIA | 0.025000 |
| PUEBLO NUEVO | 0.025000 |
Centralidad por cercanía o proximidad
Mide la distancia media de un nodo a cualquier otro nodo del grafo.
El algoritmo nos da la inversa de la distancia, por lo que los nodos que tengan la mayor puntuación tendrán, de media, distancias más cortas con el resto de los nodos que conforman el grafo.
Este algoritmo es muy interesante ya que en otro tipo de análisis, redes sociales de nuevo, nos indicaría que nodos pueden transmitir información de una forma más eficiente.
En nuestro caso, vamos a ver las estaciones que de media tienen un menor número de estaciones de distancia a cualquier otra de la red de Metro. No tenemos en cuenta el peso que sería la distancia medida en segundos.
# Centralidad de proximidad
pd.DataFrame.from_dict(nx.closeness_centrality(G2),
orient='index',
columns = ['centralidad_proximidad']) \
.sort_values(['centralidad_proximidad'], ascending = False) \
.head(10)
| centralidad_proximidad | |
|---|---|
| GREGORIO MARAÑON | 0.111111 |
| ALONSO MARTINEZ | 0.111060 |
| TRIBUNAL | 0.108499 |
| AVENIDA DE AMERICA | 0.108157 |
| NUÑEZ DE BALBOA | 0.106525 |
| RUBEN DARIO | 0.105727 |
| BILBAO | 0.105402 |
| NUEVOS MINISTERIOS | 0.105263 |
| PLAZA DE ESPAÑA | 0.105217 |
| DIEGO DE LEON | 0.104167 |
Centralidad de intermedicación
Esta es una medida de centralidad que cuantifica la frecuencia o el número de veces que un nodo actúa o sirve de puente dentro de una ruta corta entre dos nodos determinados.
Cuando en un grafo existen nodos de alta intermediación, estos suelen jugar un rol importante en la estructura a la que pertenecen. Estos nodos también poseen capacidades de ser controladores o reguladores de los flujos de información dentro de la estructura total del grafo. Esto es interesante de nuevo para aplicarlo en redes sociales.
Vamos a ver qué estaciones actúan de puente con mayor frecuencia entre las rutas más cortas del grafo.
# Centralidad intermediación
pd.DataFrame.from_dict(nx.algorithms.centrality.betweenness_centrality(G2),
orient='index',
columns = ['centralidad_intermedio'])\
.sort_values(['centralidad_intermedio'],
ascending = False)\
.head(10)
| centralidad_intermedio | |
|---|---|
| GREGORIO MARAÑON | 0.322637 |
| ALONSO MARTINEZ | 0.310687 |
| NUEVOS MINISTERIOS | 0.307194 |
| PRINCIPE PIO | 0.290740 |
| AVENIDA DE AMERICA | 0.282168 |
| PLAZA DE ESPAÑA | 0.255711 |
| CASA DE CAMPO | 0.255279 |
| TRIBUNAL | 0.244214 |
| LAGO | 0.238984 |
| BATAN | 0.233550 |
3. Algoritmo Dijkstra
En este punto vamos a utilizar al algoritmo Dijkstra para hallar la ruta más corta entre 2 estaciones. Este algoritmo tiene en cuenta el peso que tiene cada arista, por lo que el camino será establecido por el menor coste en segundos.
Hay que recordar que el tiempo que le dimos a un transbordo es de tan solo 120 segundos. Cambiando esta medida obtendríamos otros resultados.
Para poder “jugar” con el algoritmo un poco más dinámicamente vamos a utilizar widgets de IPython, y podremos ir cambiando las estaciones para ver los resultados.
En primer lugar vamos a crear una nueva lista con las líneas y las estaciones, pero en este caso con las estaciones sin las líneas asociadas, ya que para nosotros cada estación es única.
# Creamos un diccionario vacío
ESTACIONES_LINEA = {}
# Con un bucle cargamos los datos en el diccionario
for li in lineas:
ESTACIONES_LINEA['linea' + str(li)] = estaciones['estacion'].values[estaciones['linea'] == li]
# Cargamos las librerías necesarias
from IPython.html import widgets
from IPython.display import display
# Definimos algunas funciones para los widgets
def print_linea_origen(Estacion_origen):
return Estacion_origen
def select_estacion_origen(Linea_origen):
ESTACIONES_ORIGEN.options = ESTACIONES_LINEA[Linea_origen]
def print_linea_destino(Estacion_destino):
return Estacion_destino
def select_estacion_destino(Linea_destino):
ESTACIONES_DESTINO.options = ESTACIONES_LINEA[Linea_destino]
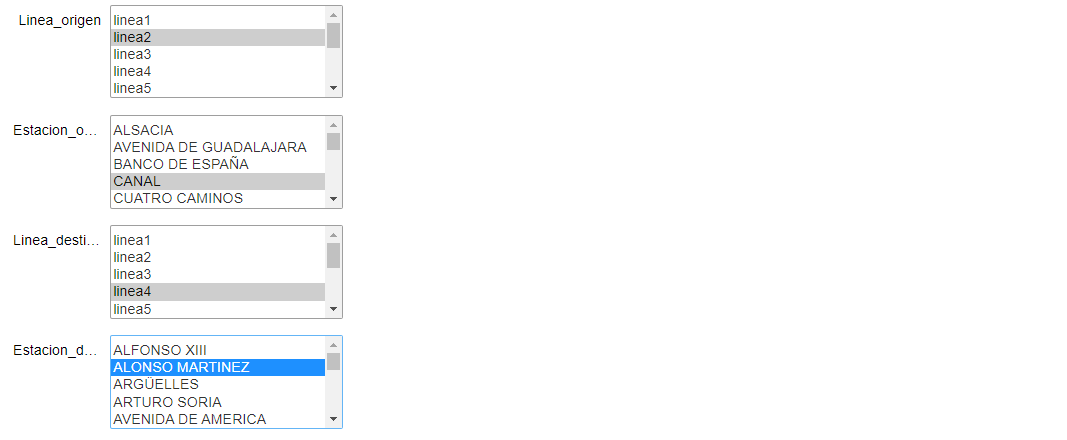
# Lanzamos los widgets
LINEAS_ORIGEN = widgets.Select(options = ESTACIONES_LINEA.keys())
ESTACIONES_ORIGEN = widgets.Select(options = ESTACIONES_LINEA[LINEAS_ORIGEN.value])
LINEAS_DESTINO = widgets.Select(options = ESTACIONES_LINEA.keys())
ESTACIONES_DESTINO = widgets.Select(options = ESTACIONES_LINEA[LINEAS_DESTINO.value])
linea_origen = widgets.interactive(select_estacion_origen, Linea_origen = LINEAS_ORIGEN)
origen = widgets.interactive(print_linea_origen, Estacion_origen = ESTACIONES_ORIGEN)
linea_destino = widgets.interactive(select_estacion_destino, Linea_destino = LINEAS_DESTINO)
destino = widgets.interactive(print_linea_destino, Estacion_destino = ESTACIONES_DESTINO)
display(linea_origen)
display(origen)
display(linea_destino)
display(destino)
# Definimos la función que utilizaremos para buscar la ruta adecuada. En este caso como puede haber varias
# rutas en origen, y varias en destino iremos probando para obtener la más corta
def buscar_ruta(origen, destino, estaciones = estaciones):
lista_origen = estaciones[estaciones['estacion'] == origen] ['estacion_linea'].to_list()
lista_destino = estaciones[estaciones['estacion'] == destino]['estacion_linea'].to_list()
ruta_seleccionada = []
for orig in lista_origen:
for dest in lista_destino:
ruta_posible = nx.dijkstra_path(G, orig, dest)
print(ruta_posible)
if len(ruta_seleccionada) == 0:
ruta_seleccionada = ruta_posible
elif len(ruta_posible) < len(ruta_seleccionada):
ruta_seleccionada = ruta_posible
return ruta_seleccionada
#Lanzamos nuestra función (Como comentábamos hay varias estaciones en origen y destino, dejamos el print para ver las posibles rutas)
ruta = buscar_ruta(origen.result, destino.result)
['CANAL_2', 'QUEVEDO_2', 'SAN BERNARDO_2', 'SAN BERNARDO_4', 'BILBAO_4', 'ALONSO MARTINEZ_4']
['CANAL_2', 'QUEVEDO_2', 'SAN BERNARDO_2', 'SAN BERNARDO_4', 'BILBAO_4', 'ALONSO MARTINEZ_4', 'ALONSO MARTINEZ_5']
['CANAL_2', 'CANAL_7', 'ALONSO CANO_7', 'GREGORIO MARAÑON_7', 'GREGORIO MARAÑON_10', 'ALONSO MARTINEZ_10']
['CANAL_7', 'ALONSO CANO_7', 'GREGORIO MARAÑON_7', 'GREGORIO MARAÑON_10', 'ALONSO MARTINEZ_10', 'ALONSO MARTINEZ_4']
['CANAL_7', 'ALONSO CANO_7', 'GREGORIO MARAÑON_7', 'GREGORIO MARAÑON_10', 'ALONSO MARTINEZ_10', 'ALONSO MARTINEZ_5']
['CANAL_7', 'ALONSO CANO_7', 'GREGORIO MARAÑON_7', 'GREGORIO MARAÑON_10', 'ALONSO MARTINEZ_10']
# Convertimos en dataframe
ruta = pd.DataFrame(ruta, columns =['estacion_linea'])
# Hacemos un merge para asignarle las coordenadas a cada estación
df_ruta = pd.merge(ruta, estaciones, how = 'left')
df_ruta
| estacion_linea | id | estacion | linea | transbordo | lat | long | |
|---|---|---|---|---|---|---|---|
| 0 | CANAL_7 | 21 | CANAL | 7 | SI | 40.438700 | -3.704894 |
| 1 | ALONSO CANO_7 | 20 | ALONSO CANO | 7 | NO | 40.438374 | -3.699255 |
| 2 | GREGORIO MARAÑON_7 | 19 | GREGORIO MARAÑON | 7 | SI | 40.438249 | -3.691495 |
| 3 | GREGORIO MARAÑON_10 | 19 | GREGORIO MARAÑON | 10 | SI | 40.437530 | -3.691276 |
| 4 | ALONSO MARTINEZ_10 | 20 | ALONSO MARTINEZ | 10 | SI | 40.428526 | -3.696442 |
Por último, vamos a graficar la ruta más corta
G3 = nx.Graph()
pos = {}
for i in range(0, len(df_ruta['estacion_linea'])):
pos[df_ruta.iloc[i, 0]] = (df_ruta.iloc[i, 6], df_ruta.iloc[i, 5])
for i in range(0, len(df_ruta['estacion_linea'])):
G3.add_edge(ruta['estacion_linea'][i], ruta['estacion_linea'][i + 1])
color = colorear_nodos(G3)
color_edge = colorear_edges(G3)
fig, ax = plt.subplots(figsize = (20,8))
nx.draw(G3,
pos = pos,
font_size = 10,
node_color = color,
node_size = 300,
edge_color = color_edge)
mplleaflet.display(fig=ax.figure)